Schwerpunkte

  • Koordination von Reverse Supply Chains

    Die Koordination von Reverse Supply Chains ...

    1. ...
    2. ...
       

    Text

    Promotionsvorhaben:

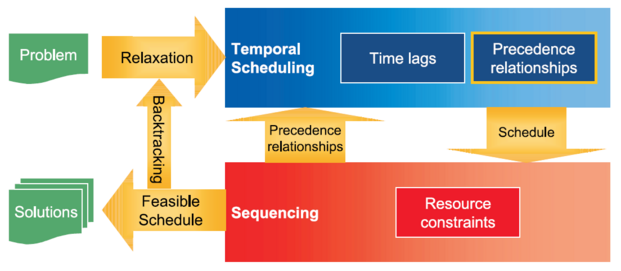
  • Ressourcenbeschränkte Scheduling-Probleme

    Pfeildiagramm

    Ein Scheduling-Problem besteht darin, unter Berücksichtigung der beschränkten Verfügbarkeit von Produktionsfaktoren die Ausführungszeitintervalle für eine Menge von Vorgängen festzulegen. In der Planung der betrieblichen Wertschöpfung treten Scheduling-Probleme als Projektplanungsprobleme in Forschung und Entwicklung und als Probleme der Termin- und Kapazitätsplanung sowie der Maschinenbelegungsplanung in der Produktionsplanung auf. Bei einem ressourcenbeschränkten Scheduling-Problem nehmen Vorgänge für ihre Ausführung typischerweise jeweils mehr als eine Einheit von Produktionsfaktoren in Anspruch. Die Produktionsfaktoren werden dann Ressourcen genannt, wobei die erneuerbaren Ressourcen den Potential- und die Lagerressourcen den Repetierfaktoren entsprechen. 

    Im Rahmen unserer Forschung führen wir für unterschiedliche Typen ressourcenbeschränkter Scheduling-Probleme grundlegende Strukturuntersuchungen durch, auf deren Grundlage wir exakte und heuristische Lösungsverfahren entwickeln. Hierzu gehören insbesondere Methoden zur Planung von Projekten, die komplexen Randbedingungen wie zeitlichen Mindest- und Höchstabständen zwischen den Aktivitäten, überlappungsabhängigen Aktivitätsdauern oder unterbrechbaren Aktivitäten unterliegen. Das von uns entwickelte Konzept der Lagerressourcen erlaubt die Integration von Materialverfügbarkeits- und Lagerkapazitätsbedingungen, die bei vielen praktischen Scheduling-Problemen eine wesentliche Rolle spielen. Scheduling-Probleme mit Lagerressourcen haben weltweit Eingang in zahlreiche Forschungsvorhaben anderer Arbeitsgruppen und in industrielle Planungssysteme gefunden.

    Promotionsvorhaben:

    Benchmark-Instanzen: Projekt-Generator ProGen/max

     

  • Integrierte Routing- und Scheduling-Probleme

    Bei der Planung der Ausführung von Vorgängen, die verschiedenen Standorten in einem Netzwerk zugeordnet sind und gemeinsame Ressourcen nutzen, müssen Entscheidungen über die Ausführungszeitintervalle der Vorgänge (Scheduling-Problem) und den Transport von Ressourceneinheiten zwischen den Standorten (Routing-Problem) getroffen werden. Solche Routing- und Scheduling-Probleme treten beispielsweise bei der Planung standortübergreifender Produktionsprozesse in Supply Chains, der Planung ambulanter Pflegedienste oder der Planung eines räumlich verteilten Projekt-Portfolios auf. Aufgrund der starken Interdependenzen zwischen den Scheduling- und Routing-Entscheidungen führt die hierarchische Zerlegung in zwei Teilprobleme häufig zu ineffizienten Lösungen. Werden die beiden Teilprobleme in einem gemeinsamen Modell betrachtet, liegt ein integriertes Routing- und Scheduling-Problem vor. Ein solches integriertes Problem ist aufgrund der höheren inhärenten Komplexität schwerer zu lösen, bildet jedoch die Potentiale einer optimalen Abstimmung zwischen Scheduling- und Routing-Entscheidungen vollständig ab.

    In unserer Forschung entwickeln wir mit dem Ressourcentransferproblem einen generischen Modellierungsrahmen für integrierte Routing- und Scheduling-Probleme. Das Ressourcentransferproblem besteht darin, die Eintrittzeitpunkte räumlich verteilter Ereignisse zu bestimmen, die die Verfügbarkeit von erneuerbaren und von Lagerressourcen beeinflussen. Jedem Ereignis sind dabei Mengen geeigneter Ressourceneinheiten zuzuordnen. Für Paare von Ereignissen müssen weiterhin zeitliche Mindest- und Höchstabstände, Transferzeiten für gemeinsam genutzte Ressourceneinheiten sowie Inkompatibilitäts- und Inklusionsbeziehungen der allozierten Ressourcenmengen beachtet werden. Eine Vielzahl verschiedener Probleme aus den Bereichen der Tourenplanung, der Maschinenbelegungsplanung und der ressourcenbeschränkten Projektplanung sowie deren Kombinationen können in diesem Referenzmodell abgebildet und zahlreiche Anforderungen praktischer Routing- und Scheduling-Probleme berücksichtigt werden. Neben der Modellentwicklung beschäftigen wir uns mit der Konzeption Constraint-basierter Lösungsverfahren für Ressourcentransferprobleme.

    Promotionsvorhaben:

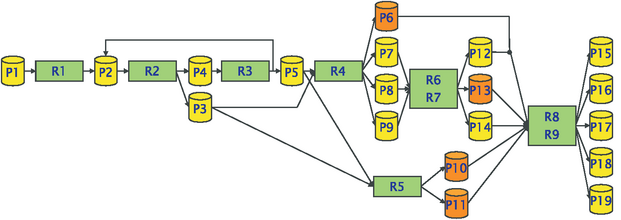
  • Anlagenbelegungsplanung in der Prozessindustrie

    Process Scheduling

    Gegenstand der Anlagenbelegungsplanung ist die kurzfristige Ressourceneinsatzplanung mehrstufiger verfahrenstechnischer Anlagen, in denen nacheinander oder gleichzeitig verschiedene Produkte hergestellt werden können. Solche Anlagen dienen der Produktion von hochwertigen Fein- und Spezialchemikalien sowie Wirkstoffen, deren Absatzmengen vergleichsweise gering und zeitlich schwankend sind. Hinsichtlich des Repetitionstyps der Produktion kann hierbei zwischen einer marktbezogenen Sortenproduktion von Produktvarianten auf Mehrproduktanlagen und einer auftragsgebundenen Chargenproduktion verschiedenartiger Produktfamilien auf Mehrzweckanlagen unterschieden werden. Die Sortenproduktion ist dabei typischerweise von einer kontinuierlichen Prozessführung und einem Anlagenbetrieb in Kampagnenfahrweise gekennzeichnet, während die Chargenproduktion häufig mit einer diskontinuierlichen Prozessführung und Mischbetrieb verbunden ist.


    Ausgangspunkt der Anlagenbelegungsplanung sind gegebene Primärbedarfe an den Endprodukten, die in mehreren Prozessschritten auf den Apparaten der betrachteten Anlage hergestellt werden. Die Anlagenbelegungsplanung umfasst die Ermittlung einer geeigneten Menge notwendiger Prozessschrittausführungen (Mengenplanung) und deren zeitliche Einplanung auf den Apparaten der Anlage (Ablaufplanung). Hierbei sind zahlreiche technologische Besonderheiten der verfahrenstechnischen Produktion wie Mischungs- und Kuppelproduktion, untere und obere Schranken für Chargengrößen, flexible Einsatzmengen- und Ausbringungsmengenverhältnisse, variable Produktionsraten oder Dauern von Prozessschritten, reihenfolgeabhängige Umrüst- und Reinigungszeiten, beschränkte Lagerkapazitäten sowie Verfalls- und Nachliegezeiten für Zwischenprodukte zu beachten. Probleme der Anlagenbelegungsplanung weisen daher eine erhebliche Komplexität auf.

    In unserer Forschung entwickeln wir leistungsfähige Verfahren für die Belegungsplanung von flexiblen Mehrzweck- und von Mehrproduktanlagen bei Chargen- und bei Sortenproduktion. Im Unterschied zu den in der Literatur dokumentierten Totalmodellen der gemischt-ganzzahligen Optimierung verfolgen wir einen hierarchischen Dekompositionsansatz, der die Planungsaufgabe in die Mengen- und die Ablaufplanung zerlegt. Zur Mengenplanung werden geeignete Modellierungstechniken und Methoden der gemischt-ganzzahligen linearen und nichtlinearen Optimierung eingesetzt. Vor dem Hintergrund unsicherer Planungsdaten werden für die Anlagenbelegungsplanung Ansätze der prädiktiv-reaktiven Planung untersucht, die Verfahren zur Mengen- und Verfahren zur Ablaufplanung unter Unsicherheit geeignet miteinander kombinieren. Für Echtzeit-Anwendungen der Ablaufplanung wie kurzfristige Kapazitäts-Verfügbarkeitsprüfungen werden Prioritätsregelverfahren zur Online-Optimierung eingesetzt, die eine besonders effiziente inkrementelle Einplanung von Produktionsaufträgen erlauben.

    Promotionsvorhaben:

  • Planung präventiver Instandhaltungsmaßnahmen

    Die Instandhaltung umfasst gemäß DIN 31051 alle "Maßnahmen zur Bewahrung und Wiederherstellung des Soll-Zustandes sowie zur Feststellung und Beurteilung des Ist-Zustandes von technischen Mitteln eines Systems". Zur Instandhaltung gehören die reaktiven Maßnahmen der Instandsetzung wie Reparatur oder fehlerbedingte Ersetzung von Systemen oder Komponenten sowie die präventiven Maßnahmen der Inspektion und der vorbeugenden bzw. zustandsorientierten Wartung und Ersetzung. Durch eine Instandhaltungsmaßnahme kann der Zustand einer Komponente des betrachteten Systems in einen besseren Zustand überführt werden. Der Grad der Verbesserung ist dabei von der Art und dem Umfang der Maßnahme abhängig. Das System geht durch die Instandhaltung einer Komponente in einen nicht-schlechteren Zustand über, der sich aus der Strukturfunktion des Systems ergibt. Gegenstand der Instandhaltungsplanung ist das Entscheidungsproblem, unter welchen Bedingungen an welchen Komponenten welche Instandhaltungsmaßnahmen in welchem Umfang ausgeführt werden sollten, damit ein Zielsystem im Prozess der Systemzustände über einem endlichen oder unendlichen Planungszeitraum optimiert wird.

    In unserer Forschung beschäftigen wir uns mit der Entwicklung leistungsfähiger Algorithmen der kombinatorischen sowie der stochastischen und simulationsgestützten Optimierung für die Planung der präventiven Instandhaltung komplexer technischer Systeme, die aus einer Vielzahl verbundener Komponenten bestehen. Beispiele solcher Systeme sind Infrastrukturnetzwerke wie Kommunikations-, Elektrizitäts-, Gas-, Wasser- oder Verkehrsnetze, aber auch modulare Systeme wie Maschinen oder Anlagen, deren Systemleistung in eindeutiger Weise von den Zuständen der einzelnen Komponenten abhängt. Als Ergebnis der Instandhaltungsplanung erhält man komponentenspezifische Eventualpläne im Sinne der flexiblen Planung. Dies bedeutet, dass die ermittelte Instandhaltungspolitik für jede Komponente und jede Periode in Abhängigkeit der beobachteten Zustände aller Komponenten zu Beginn der Periode festlegt, ob und falls ja, welche Wartungsmaßnahmen in welchem Umfang durchgeführt werden sollten. Dabei betrachten wir für endliche Planungszeiträume die Fälle von binären und von Multi-Zustandssystemen sowie die Fälle deterministischer und stochastischer Verschleißprozesse. Während binäre Systeme Sprungausfällen unterliegen, die mit Hilfe vorbeugender Maßnahmen weitestgehend vermieden werden sollen, untersuchen wir für Multi-Zustandssysteme den Fall von Parameterdriften, die es erlauben, das kontinuierliche Verschleißverhalten von Systemen abzubilden. Für Multi-Zustandssysteme werden Strategien der zustandsorientierten Instandhaltung erforscht.

    Promotionsvorhaben:

  • Konfigurationsplanung von Lagersystemen

    Die Konfiguration eines Lagersystems lässt sich in fünf wichtige Aufgaben gliedern:

    1. Festlegung der Lagerplatzvergabestrategie
    2. Dimensionierung und Allokation der Lagerkapazität zu Artikeln bzw. Artikelgruppen
    3. Auslegung der Lagertechnik und Layoutplanung
    4. Festlegung der Ein- und Auslagerstrategie
    5. Auslegung der Fördertechnik
       

    Während die Lagerplatzvergabestrategie das Prinzip vorgibt, nach dem den Artikeln mögliche Lagerplätze zugeordnet werden können, wird im Rahmen der Dimensionierung und Allokation der Lagerkapazität bestimmt, wie viele Lagerplätze einzurichten sind und auf welche Lagerplätze die einzelnen Artikel zugreifen können, falls keine freie Lagerplatzvergabe vorgesehen ist. Anschließend ist über die einzusetzenden Lagermittel und Lagerhilfsmittel zu entscheiden (Lagertechnik) und jedem Lagerplatz und den Ein-/Auslagerpunkten eine physische Position im Lager zuzuweisen (Layoutplanung). Die Ein- und Auslagerstrategie definiert, wie Ein- und Auslageraufträge im Betrieb grundsätzlich ausgeführt werden können. Dies umfasst die Regeln zur Bildung der Arbeitsspiele der Fördermittel und die Regeln, nach denen den Aufträgen geeignete Lagerplätze zugewiesen werden. Bei der Auslegung der Fördertechnik müssen schließlich die Art, die Anzahl und die Leistungsparameter der einzusetzenden Fördermittel festgelegt werden.

    Gegenstand unserer Forschung sind Modelle und Methoden zur Unterstützung der Kapazitätsdimensionierung und -allokation sowie der Auslegung der Fördertechnik für unterschiedliche Kombinationen aus Lagerplatzvergabe- sowie Ein- und Auslagerstrategien. Dabei werden die Lagerplatzbedarfe als Zufallsvariablen und die Ankünfte von Ein- und Auslageraufträgen als stochastische Prozesse modelliert. Für die resultierenden stochastischen Optimierungs- und Analysemodelle entwickeln wir effiziente Verfahren der mathematischen Programmierung und der Kenngrößenanalyse stationärer Markov-Prozesse. In weiteren Untersuchungen interessieren wir uns für die Abhängigkeiten zwischen den einzelnen Teilproblemen der Lagerkonfiguration und Möglichkeiten, diese in einem rückgekoppelten Planungsansatz zu berücksichtigen.

    Promotionsvorhaben: