Research areas

  • Coordination of reverse supply chains

    Coordination of reverse supply chains...

    1. ...
    2. ...

    text

    PhD project:

  • Resource-constrained scheduling problems

    Pfeildiagramm

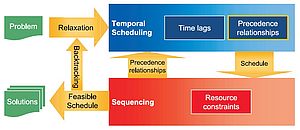
    A scheduling problem consists of determining the execution time intervals for a set of operations, taking into account the limited availability of production factors. In operational value-added planning, scheduling problems occur as project planning problems in research and development and as scheduling, capacity planning, and machine allocation planning problems in production planning. In a resource-constrained scheduling problem, operations typically take more than one unit of production factors each to execute. The factors of production are then called resources, where renewable resources correspond to potential resources and storage resources correspond to repetitive resources.

    As part of our research, we conduct fundamental structural studies for different types of resource-constrained scheduling problems, based on which we develop exact and heuristic solution methods. In particular, this includes methods for scheduling projects that are subject to complex constraints such as minimum and maximum time intervals between activities, overlap-dependent activity durations, or interruptible activities. The concept of storage resources we have developed allows the integration of material availability and storage capacity constraints, which play an essential role in many practical scheduling problems. Scheduling problems with storage resources have found their way into numerous research projects of other research groups and into industrial planning systems worldwide.

    PhD project:

    Benchmark Instances: Project Generator ProGen/max

     

  • Integrated routing and scheduling problems

    When planning the execution of operations that are assigned to different locations in a network and share resources, decisions have to be made about the execution time intervals of the operations(scheduling problem) and the transport of resource units between the locations(routing problem). Such routing and scheduling problems arise, for example, in the planning of cross-site production processes in supply chains, the planning of ambulatory care services, or the planning of a spatially distributed project portfolio. Due to the strong interdependencies between the scheduling and routing decisions, the hierarchical decomposition into two subproblems often leads to inefficient solutions. If the two subproblems are considered in a joint model, an integrated routing and scheduling problem exists. Such an integrated problem is harder to solve due to its higher inherent complexity, but fully represents the potentials of optimal coordination between scheduling and routing decisions.

    In our research, we develop the resource transfer problem as a generic modeling framework for integrated routing and scheduling problems. The resource transfer problem consists of determining the occurrence times of spatially distributed events that affect the availability of renewable and storage resources. Each event must be assigned quantities of appropriate resource units. For pairs of events, minimum and maximum time intervals, transfer times for shared resource units as well as incompatibility and inclusion relations of the allocated resource quantities have to be considered. A large number of different problems from the areas of route scheduling, machine allocation scheduling and resource-constrained project scheduling as well as their combinations can be represented in this reference model and numerous requirements of practical routing and scheduling problems can be considered. In addition to model development, we are engaged in the design of constraint-based solution procedures for resource transfer problems.

    PhD project:

  • Plant occupancy planning in the process industry

    Process Scheduling

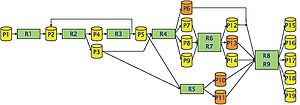
    The subject of plant utilization planning is the short-term resource utilization planning of multi-stage process plants in which different products can be manufactured successively or simultaneously. Such plants are used for the production of high-quality fine and specialty chemicals as well as active ingredients whose sales volumes are comparatively small and fluctuate over time. With regard to the repetition type of production, a distinction can be made between market-related variety production of product variants on multi-product plants and order-related batch production of different product families on multi-purpose plants. Variety production is typically characterized by continuous process control and plant operation in campaign mode, while batch production is often associated with discontinuous process control and mixed operation.

    Starting point of the plant layout planning are given primary requirements of the final products, which are produced in several process steps on the equipment of the plant under consideration. The plant layout planning includes the determination of a suitable quantity of necessary process step executions(quantity planning) and their scheduling on the equipment of the plant(sequence planning). Numerous technological peculiarities of process engineering production such as mixing and joint production, lower and upper limits for batch sizes, flexible input quantity and output quantity ratios, variable production rates or durations of process steps, sequence-dependent changeover and cleaning times, limited storage capacities as well as expiry and post-lay times for intermediate products must be taken into account. Therefore, problems of plant layout planning show a considerable complexity. In our research, we develop efficient methods for the scheduling of flexible multi-purpose and multi-product plants for both batch and variety production. In contrast to the total models of mixed-integer optimization documented in the literature, we follow a hierarchical decomposition approach, which decomposes the planning task into the quantity planning and the sequence planning. Suitable modeling techniques and methods of mixed-integer linear and nonlinear optimization are used for quantity planning. Against the background of uncertain planning data, approaches of predictive-reactive planning are investigated for plant allocation planning, which suitably combine methods for quantity planning and methods for sequence planning under uncertainty. For real-time applications of sequence planning such as short-term capacity availability checks, priority control methods for online optimization are used, which allow a particularly efficient incremental scheduling of production orders.

    PhD project:

  • Planning of preventive maintenance measures

    According to DIN 31051, maintenance includes all "measures for maintaining and restoring the target condition as well as for determining and assessing the actual condition of technical means of a system". Maintenance includes reactive measures such as repair or fault-related replacement of systems or components as well as preventive measures such as inspection and preventive or condition-oriented maintenance and replacement. A maintenance task can change the condition of a component of the system under consideration into a better condition. The degree of improvement depends on the type and scope of the task. As a result of the maintenance of a component, the system changes to a non-worse condition, which results from the structural function of the system. The object of maintenance planning is the decision problem under which conditions on which components which maintenance actions should be performed to what extent, so that a target system is optimized in the process of system states over a finite or infinite planning period.

    In our research, we are concerned with the development of powerful algorithms of combinatorial as well as stochastic and simulation-based optimization for the planning of preventive maintenance of complex technical systems that consist of a large number of connected components. Examples of such systems are infrastructure networks such as communication, electricity, gas, water or traffic networks, but also modular systems such as machines or plants whose system performance depends in a unique way on the states of the individual components. The result of maintenance planning is component-specific contingency plans in the sense of flexible planning. This means that the determined maintenance policy for each component and each period determines, depending on the observed states of all components at the beginning of the period, whether and, if so, which maintenance tasks should be performed and to what extent. Here, for finite planning periods, we consider the cases of binary and of multi-state systems as well as the cases of deterministic and stochastic wear processes. While binary systems are subject to step failures, which should be avoided as far as possible by means of preventive measures, we investigate the case of parameter drifts for multi-state systems, which allow us to map the continuous wear behaviour of systems. For multi-state systems, strategies of condition-based maintenance are investigated.

    PhD project:

  • Configuration planning of storage systems

    Configuring a storage system can be broken down into five major tasks:

    1. Determining the storage bin allocation strategy
    2. Dimensioning and allocation of storage capacity to articles or article groups
    3. Design of the storage technology and layout planning
    4. Determination of the storage and retrieval strategy
    5. Design of the conveyor system

    While the storage bin assignment strategy defines the principle according to which possible storage bins can be assigned to the articles, the dimensioning and allocation of the storage capacity determines how many storage bins are to be set up and which storage bins the individual articles can access if no free storage bin assignment is planned. Next, a decision must be made about the storage media and storage aids to be used (storage technology) and a physical position in the warehouse must be assigned to each storage bin and the putaway/retrieval points (layout planning). The putaway and picking strategy defines how putaway and picking orders can basically be executed in the site. This includes the rules for forming the work cycles of the conveyors and the rules according to which suitable storage bins are assigned to the orders. Finally, the type, number and performance parameters of the conveyors to be used must be determined in the design of the conveyor system.

    The subject of our research are models and methods to support capacity dimensioning and allocation as well as the design of the conveyor system for different combinations of storage bin allocation as well as storage and retrieval strategies. In this context, the storage space requirements are modeled as random variables and the arrivals of storage and retrieval orders as stochastic processes. For the resulting stochastic optimization and analysis models we develop efficient methods of mathematical programming and characteristic analysis of stationary Markov processes. In further investigations, we are interested in the dependencies between the individual subproblems of the bearing configuration and possibilities to consider them in a feedback planning approach.

    PhD project: